わたしの愛してやまない漫才師「金属バット」。

彼らの漫才の中に以下のような件があります。

 

 

「円周率ってさ・・・２なんすよ」

「バグってんのか！」

「ちょうど２」

「２なわけあるかい！３で手打ちで大揉めやってんで？」

 

その後円周率が２である根拠を次々に披露していくという展開。

終盤では

「教育を疑え」「概念つぶしていけ」

という痺れる言葉・・・。

もちろんこれを漫才のネタとして長年楽しんできたのですが、つい先日”円周率が本当に２になる場合もある”という事実を知ってしまったので解説してみたいと思います。

 

 

まず、前提として

①円周率とは、円周の直径に対する比（円周率＝円周÷直径）である

②円とは、ある1点（中心）から等距離の点を結んでできる図形である

③曲面上の円では2点間の最短距離を半径とする

ということを確認しておきます。

そうです。曲面上（球体）にて円を考えてみたいと思います。

 

まず図１のように半径rの円の天頂に点Oを取ります。そしてそこから円周の1/4離れた位置に点Aを取ります。

 

 

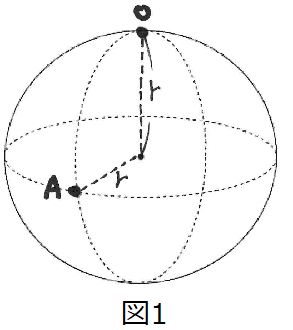
このOAを半径と考えると、OAと長さの等しい点が図２のようにたくさん見つかります。これらを結んだの円（図3青色）が中心O、半径OAの円となります。

 

 

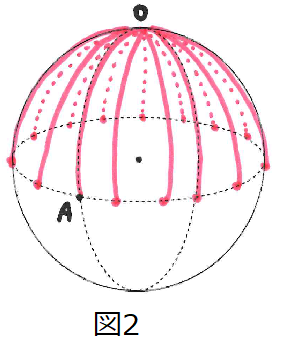
ここで半径OAは、半径ｒの円の円周の1/4ですので1/4×ｒ^2×π

と表せられるので、直径はその２倍で1/2×ｒ^2×π

そして円周は半径ｒの円と同じなのでｒ^2×πとなります。

図３でいうと赤色が直径、青色が円周ということになります。

 

 

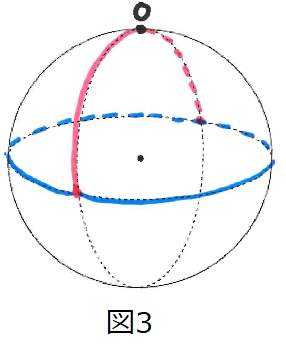
つまりこの円の円周率は

（ｒ^2×π）÷（1/2×ｒ^2×π）＝２

となります！！

見事、漫才内に語られた方法以外で円周率＝２を導きました！

 

Ｍ－１ラストイヤーで準決勝当日に療養から復帰というドラマと作りながらも惜しくも敗退した金属バットを個別指導いしきは（正確には塾長個人が）応援しております。

 

お疲れっした～